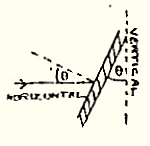
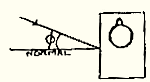
The Angle of Impact on Armour Plate with the Angle of Attack in the Horizontal Plane
Formula: Cosine (Compound Angle) = Cosine (Vertical Angle) x Cosine (Horizontal Angle)
This information above was supplied to me by Jim O’Neil (Arizona, USA), the original source was Lorrin Bird. I’ve added a couple of quick comments below in the Notes section.
| TARGET PLATE Fig.1 | ANGLE OF ATTACK IN HORIZONTAL PLANE Fig.2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5º | 10º | 15º | 20º | 25º | 30º | 40º | 50º | 60º | 70º | |
| 5º | 7º 3′ | 11º 8′ | 15º 48′ | 20º 34′ | 25º 24′ | 30º 23′ | 40º 14′ | 50º 6′ | 60º 5′ | 70º 5′ |
| 10º | 11º 8′ | 14º 4′ | 17º 57′ | 22º 16′ | 26º 45′ | 31º 28′ | 41º 2′ | 50º 46′ | 60º 30′ | 70º 17′ |
| 15º | 15º 48′ | 17º 57′ | 21º 5′ | 24º 47′ | 28º 49′ | 33º 13′ | 42º 16′ | 51º 30′ | 61º 6′ | 70º 42′ |
| 20º | 20º 34′ | 22º 16′ | 24º 47′ | 27º 58′ | 31º 33′ | 35º 30′ | 43º 58′ | 52º 47′ | 61º 58′ | 71º 9′ |
| 25º | 25º 24′ | 26º 45′ | 28º 49′ | 31º 33′ | 34º 42′ | 38º 15′ | 46º 1′ | 54º 18′ | 63º 2′ | 71º 51′ |
| 30º | 30º 23′ | 31º 28′ | 33º 13′ | 35º 30′ | 38º 15′ | 41º 25′ | 48º 26′ | 56º 10′ | 64º 19′ | 72º 46′ |
| 40º | 40º 14′ | 41º 2′ | 42º 16′ | 43º 58′ | 46º 1′ | 48º 26′ | 54º 5′ | 60º 31′ | 67º 28′ | 76º 35′ |
| 50º | 50º 6′ | 50º 46′ | 51º 30′ | 52º 47′ | 54º 18′ | 56º 10′ | 60º 31′ | 65º 36′ | 71º 15′ | 77º 18′ |
| 60º | 60º 5′ | 60º 30′ | 61º 6′ | 61º 58′ | 63º 2′ | 64º 19′ | 67º 28′ | 71º 15′ | 75º 30′ | 80º 3′ |
| 70º | 70º 5′ | 70º 17′ | 70º 42′ | 71º 9′ | 71º 51′ | 72º 46′ | 76º 35′ | 77º 18′ | 80º 3′ | 83º18′ |
Notes
This table shows the “real” angle of plate based on the firer’s angle of attack in the horizontal plane. For example an M4 Sherman comes barrelling around a corner in the Bocage, and encounters a Tiger II. The King Tiger is 150 yards away, and the Sherman is off centre. Let us say the Sherman is at an angle of 40º from directly in front of the King Tiger. The Sherman is faced with a Tank that has front superstructure armour of 150mm, but it is at an angle of 50º, so its real horizontal plane thickness is 233mm. But because we are at a 40º angle the equivalent slope of the armour is 60½º giving an equivalent horizontal plane thickness of 304mm – Boy is that Sherman in trouble! Note how the angle has more than doubled the thickness of the Armour Plate!
This of course assumes both vehicles are on perfectly level ground, and does not take account of the actual angle of impact for the projectile (over 150 yards there should basically be no “dipping” of the projectile nose to alter the angle). This could easily increase the angle if the Target (the Tiger) is on marginally higher ground than the Firer (the Sherman).